Introduction to Chi-Square Distribution ~ University Notes

The chi-square (

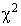
) distribution is obtained from the values of the ratio of the sample variance and population variance multiplied by the degrees of freedom. This occurs when the population is normally distributed with population variance sigma^2.

Properties of the Chi-Square

Chi-square is non-negative. Is the ratio of two non-negative values, therefore must be non-negative itself.
Chi-square is non-symmetric.
There are many different chi-square distributions, one for each degree of freedom.
The degrees of freedom when working with a single population variance is n-1.

Chi-Square Probabilities

Since the chi-square distribution isn't symmetric, the method for looking up left-tail values is different from the method for looking up right tail values.

Area to the right - just use the area given.
Area to the left - the table requires the area to the right, so subtract the given area from one and look this area up in the table.
Area in both tails - divide the area by two. Look up this area for the right critical value and one minus this area for the left critical value.

DF which aren't in the table

When the degrees of freedom aren't listed in the table, there are a couple of choices that you have.

You can interpolate. This is probably the more accurate way. Interpolation involves estimating the critical value by figuring how far the given degrees of freedom are between the two df in the table and going that far between the critical values in the table. Most people born in the 70's didn't have to learn interpolation in high school because they had calculators which would do logarithms (we had to use tables in the "good old" days).
You can go with the critical value which is less likely to cause you to reject in error (type I error). For a right tail test, this is the critical value further to the right (larger). For a left tail test, it is the value further to the left (smaller). For a two-tail test, it's the value further to the left and the value further to the right. Note, it is not the column with the degrees of freedom further to the right, it's the critical value which is further to the right.