Scheffé Test

When the decision from the One-Way Analysis of Variance is to reject the null hypothesis, it means that at least one of the means isn't the same as the other means. What we need is a way to figure out where the differences lie, not just that there is a difference.
This is where the Scheffe' and Tukey tests come into play. They will help us analyze pairs of means to see if there is a difference -- much like the difference of two means covered earlier.

Hypotheses

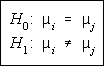Both tests are set up to test if pairs of means are different. The formulas refer to mean i and mean j. The values of i and j vary, and the total number of tests will be equal to a combination of k objects, 2 at a time C(k,2), where k is the number of samples.

Scheffé Test

The Scheffe' test is customarily used with unequal sample sizes, although it could be used with equal sample sizes.
The critical value for the Scheffe' test is the degrees of freedom for the between variance times the critical value for the one-way ANOVA. This simplifies to be:

   CV = (k-1) F(k-1,N-k,alpha)

The test statistic is a little bit harder to compute. 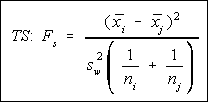Pure mathematicians will argue that this shouldn't be called F because it doesn't have an F distribution (it's the degrees of freedom times an F), but we'll live it with it.
Reject H₀ if the test statistic is greater than the critical value. Note, this is a right tail test. If there is no difference between the means, the numerator will be close to zero, and so performing a left tail test wouldn't show anything.